1) Densidad y peso especifico.-
La densidad es la medida de la masa contenida en la unidad de volumen; la unidad de medida en el sistema práctico es Kg/m3 .
El peso específico suministra el peso de la unidad del volumen en el sistema práctico es medido en
Entre las dos grandezas subsiste la conocida relación:
el modulo de la aceleración de la gravedad por la cual en el territorio Italiano, puede asumir el valor constante de 9,81 m/s2 .
La densidad y el peso específico de un fluido son función sea de la presión p que de la temperatura ; la relación:
2) Estática de los fluidos pesantes e incompresible.
Se toma en consideración un fluido quieto ( sin movimiento ) sujeto únicamente a la acción del campo gravitacional. La fuerza de masa es obviamente conservativa, e indicada con z la cuota geodésica del genérico punto, medido sobre donde se quiera de un plano horizontal referido ( superficie equipotencial, si se considera una extensión espacial no demasiado grande, como resulta en cuestiones de interés técnico) ella resulta expresa de la relación:
F= - g grad z ,
Donde la aceleración de gravedad g es supuesta constante.
Admitamos en otro que el fluido sea incompresible e isotérmico, que la densidad sea independiente de la presión y constante en toda la masa fluida. Esta hipótesis es plenamente aceptable en práctica por todos los líquidos, lo cual la compresibilidad, como ya se ha dicho, es muy pequeña.
La formula :
ecuación fundamental de la estática de los fluidos pesados e incompresible o ley de Stevin.
La grandeza
se da el nombre de cota piezométrica.
La fórmula 2.4 entonces indica que todos los puntos de un fluido pesados incompresible en reposo compete la misma cota piezométrica, el cual el valor es determinado cuando sea asignado la presión en un punto de dicha cota z . Con esto resulta completamente determinada la distribución de la presión en toda la masa fluida.
De la fórmula 2.4 se reconoce inmediatamente que la superficie isobárica ( p= cost. ) están en un plano horizontal, como el resto puede ya deducirse del hecho que tal son superficie equipotencial del campo gravitacional. La constante de integración que figura en la (2.4) representa obviamente la cota del plano horizontal en los cuales los puntos la presión es nula.
Sea A y B dos puntos cualquiera adyacentes respectivamente sus dos planos horizontales de cota za y zb, la relación entre las presiones pa y pb resulta de la aplicación de la (2.4).
Pb= pa + ( za - zb ) (2-5)
La presión aumenta es decir linealmente al disminuir la cota geodésica, con el factor de proporcionalidad igual al peso especifico del fluido.
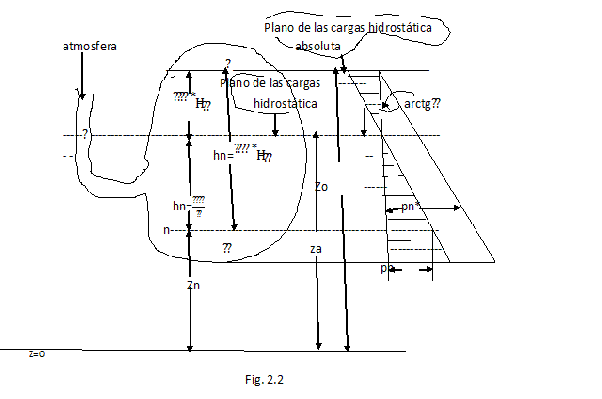
Consideremos cualquier recipiente cerrado conteniendo un liquido de pnpeso especifico ( fig. 2.2 ) y sea pn* la presión absoluta en el (*) en el punto N de cota zn, y admitamos que ella sea mayor de aquella atmosférica.
Los puntos con cota genérica z zn competen obviamente a presiones inferiores a del punto N; existirá en consecuencia un plano horizontal de cota za sobre el cual la presión es exactamente igual a la presión atmosférica pa*; la cota za se obtiene aplicando la ( 2.5 ) y vale:
La posición de esta plano, el cual se da el nombre de plano de las cargas hidrostática ,
Hn= ‘pn/pesp, (p*n= presión absoluta en el punto n), (pesp= peso especifico del liquido ) , hn= pn/ pesp ( donde pn es la presión ejercida por el liquido en el punto n )
Es claramente individuales imaginando conectado al recipiente un tubo superiormente en comunicación con la atmosfera; dentro del tubo el liquido se alza hasta la cota za , porque sobre la superficie actua la presión atmosférica pa*.
Si consideramos puntos a cota superior a za la presión en esa es obviamente inferior a la atmosférica y puede individuarse un plano a cota zo sobre la cual la presión sea nula; siempre dela ( 2.5 ), se obtiene
zo= zn + (p*-p*a)/ pesp
Este plano, denominado plano de las cargas hidrostática absoluto, debiera corresponder a la superficie libre del liquido contenida el recipiente, y de sobre de el deberá tener el vacio, porque como ya dicho, los fluidos en general no resisten los esfuerzos de tracción y por esto no pueden ser sujetado a presión absoluta negativa.
En verdad puede observarse que la superficie libre antes dicha coincide no exactamente con el plano de las cargas hidrostática absoluto, pero se encuentra a cota inferior, porque el espacio sobre de esa resulta siempre ocupado de los vapores del liquido, con una cierta tensión de vapores.
La distancia entre los dos planos de las cargas hidrostática así definida vale:
zo- za= p*a/pesp=
2) Estática de los fluidos pesantes e incompresible.
Se toma en consideración un fluido quieto ( sin movimiento ) sujeto únicamente a la acción del campo gravitacional. La fuerza de masa es obviamente conservativa, e indicada con z la cuota geodésica del genérico punto, medido sobre donde se quiera de un plano horizontal referido ( superficie equipotencial, si se considera una extensión espacial no demasiado grande, como resulta en cuestiones de interés técnico) ella resulta expresa de la relación:
F= - g grad z ,
Donde la aceleración de gravedad g es supuesta constante.
Admitamos en otro que el fluido sea incompresible e isotérmico, que la densidad sea independiente de la presión y constante en toda la masa fluida. Esta hipótesis es plenamente aceptable en práctica por todos los líquidos, lo cual la compresibilidad, como ya se ha dicho, es muy pequeña.
La formula :
ecuación fundamental de la estática de los fluidos pesados e incompresible o ley de Stevin.
La grandeza
se da el nombre de cota piezométrica.
La fórmula 2.4 entonces indica que todos los puntos de un fluido pesados incompresible en reposo compete la misma cota piezométrica, el cual el valor es determinado cuando sea asignado la presión en un punto de dicha cota z . Con esto resulta completamente determinada la distribución de la presión en toda la masa fluida.
De la fórmula 2.4 se reconoce inmediatamente que la superficie isobárica ( p= cost. ) están en un plano horizontal, como el resto puede ya deducirse del hecho que tal son superficie equipotencial del campo gravitacional. La constante de integración que figura en la (2.4) representa obviamente la cota del plano horizontal en los cuales los puntos la presión es nula.
Sea A y B dos puntos cualquiera adyacentes respectivamente sus dos planos horizontales de cota za y zb, la relación entre las presiones pa y pb resulta de la aplicación de la (2.4).
Pb= pa + ( za - zb ) (2-5)
La presión aumenta es decir linealmente al disminuir la cota geodésica, con el factor de proporcionalidad igual al peso especifico del fluido.
Consideremos cualquier recipiente cerrado conteniendo un liquido de pnpeso especifico ( fig. 2.2 ) y sea pn* la presión absoluta en el (*) en el punto N de cota zn, y admitamos que ella sea mayor de aquella atmosférica.
Los puntos con cota genérica z zn competen obviamente a presiones inferiores a del punto N; existirá en consecuencia un plano horizontal de cota za sobre el cual la presión es exactamente igual a la presión atmosférica pa*; la cota za se obtiene aplicando la ( 2.5 ) y vale:
La posición de esta plano, el cual se da el nombre de plano de las cargas hidrostática ,
Hn= ‘pn/pesp, (p*n= presión absoluta en el punto n), (pesp= peso especifico del liquido ) , hn= pn/ pesp ( donde pn es la presión ejercida por el liquido en el punto n )
Es claramente individuales imaginando conectado al recipiente un tubo superiormente en comunicación con la atmosfera; dentro del tubo el liquido se alza hasta la cota za , porque sobre la superficie actua la presión atmosférica pa*.
Si consideramos puntos a cota superior a za la presión en esa es obviamente inferior a la atmosférica y puede individuarse un plano a cota zo sobre la cual la presión sea nula; siempre dela ( 2.5 ), se obtiene
zo= zn + (p*-p*a)/ pesp
Este plano, denominado plano de las cargas hidrostática absoluto, debiera corresponder a la superficie libre del liquido contenida el recipiente, y de sobre de el deberá tener el vacio, porque como ya dicho, los fluidos en general no resisten los esfuerzos de tracción y por esto no pueden ser sujetado a presión absoluta negativa.
En verdad puede observarse que la superficie libre antes dicha coincide no exactamente con el plano de las cargas hidrostática absoluto, pero se encuentra a cota inferior, porque el espacio sobre de esa resulta siempre ocupado de los vapores del liquido, con una cierta tensión de vapores.
La distancia entre los dos planos de las cargas hidrostática así definida vale:
zo- za= p*a/pesp p*a= presión atmosférica
es decir que la altura piezométrica corresponde a la presión atmosférica; ejemplo si el liquido es agua (peso específico=pesp =1000 Kg/m3 ) eso vale 10,33 m; si se trata de mercurio ( el peso específico del mercurio= 13600 Kg/m3 ) eso resulta 0,76 m.
si el recipiente es cerrado como en fig. 2.2 es superiormente abierto, sobre pelo libre actúa la presión atmosférica y por tanto eso viene a coincidir con el plano de las cargas hidrostática.
Salvo casos del todo particular, en lo tratados de los problemas prácticos se hace referencia a la presión relativa también a la absoluta como hecho sobre entendiéndose por presión relativa p la diferencia entre la genérica presión absoluta y aquella atmosférica : p= p* - pa presión absoluta= presión atmosférica + presión ejercida del liquido .
Suponemos conocido el plano de las cargas hidrostática ( también aquello absoluto que se encuentra a una cota mas alta de pa*/pesp) , la presión en el genérico punto de cota z vale:
Presión absoluta p*= pesp( zo- z )= pespxh*
Presión relativa p= pesp( za – z )= pespxh
Es decir la presión absoluta o relativa en un punto es igual al producto del peso especifico del fluido por el fondo del mismo punto bajo el correspondiente plano de las cargas hidrostática.
Se deriva inmediatamente que, conocida la presión del punto, el plano de las cargas hidrostática sobre el punto mismo de la altura piezométrica h .
Individuando el plano de las cargas hidrostática, es fácil trazar el diagrama de las presiones largo la vertical, por medio de cual, siendo los planos horizontales superficie isobárica, puede ser determinada las presiones en cualquier punto del fluido; basta trazar una recta inclinada de arctg sobre la vertical y con origen a la cota del plano de las cargas hidrostática ( fig. 2.2 ); los diagramas de las presiones absoluta y relativa son evidentemente paralelas entre ellos a una distancia horizontal igual a pa* y vertical igual a .
Puede suceder que en un mismo recipiente contengan más fluido no mesclado entre ellos; se dispone estratos horizontales de peso especifico creciente hacia abajo.
Supongamos de hecho que la superficie de separación entre el fluido 1 de peso especifico 1 y aquel 2 de peso especifico 2 tenga una forma cualquiera ( fig. 2.3 ) en un genérico punto M tal que la superficie la presión es igual para las dos partículas infinitamente vecina pero perteneciente a los fluidos 1 y 2. De la otra parte la presión en el punto M’ puesto a la misma cota al interno del fluido 1, es igual a aquella en M; lo mismo vale para los dos puntos N y N’. Las presiones en estos dos puntos valen
Fig. 2.3
PN= PM’ + pesp1xh
PN’= PM + pesp2xh
Pero deben ser igual entre ellos resulta:
PM + pesp1x h = PM + pesp2x h
MEDIDA DE LA PRESION:
Como hemos visto en el precedente parágrafo, es suficiente conocer la presión en un punto para individuar con facilidad la distribución de la presión en la entera masa liquida. Nos proponemos por esto a describir el siguiente aparato apto para medir la presión en un punto: mejor, a individuar la cota piezométrica de la masa fluida.
El dispositivo más simple y mas practico es el piezómetro, constituido de un tubo, vertical o inclinado, abierto en la altura y conectado en el otro extremidad del recipiente conteniendo el liquido ( Fig. 2.2) el cual, como ya dicho, si se alza en él hasta la cota del plano de las cargas hidrostática.
Si la presión del liquido es elevada y por esto las cargas hidrostática es muy alto, el dispositivo resulta de difícil situación practica es conveniente adoptar un manómetro simple, que entre otro puede ser usado con cualquier fluido. Los manómetros simples son esencialmente constituido de un tubo en U de la cual una extremidad es conectada con el recipiente que contiene el fluido y la otra está en comunicación con la atmosfera (Fig. 2.4) .
En la parte inferior del tubo U se dispone un liquido con peso especifico m superior a del fluido en el recipiente; con frecuencia se usa el mercurio con m 13.600 Kg/ .
Por efecto del estado de presiones del fluido en el recipiente, el liquido manométrico se porta a cota diversa en las dos ramas del manómetro, y se puede leer fácilmente el desnivel entre los dos puntos M y N’.
Si escribimos sobre el plano horizontal pasando por el punto M la presión es igual en las dos ramas se obtiene:
PM= PN= Vxpespm; donde V es el desnivel y pespm= es el peso especifico del mercurio
Cuando en el recipiente se tiene un liquido se obtiene en fin:
h= pm/pesp= Vxpespm/pesp
Siendo h el hondo del punto M bajo el plano de las cargas hidrostática del liquido en el recipiente.
Observando que la presión relativa en M es negativa en N’ en el ramo abierto se lleva a una cota más baja de M, el plano de las cargas hidrostática es ahora en M siempre la cantidad h= Vxpespm/ pesp
El teorema de Bernoulli.-
La cota geodésica z y la altura piezométrica , la cual la suma la suma la hemos llamado cota piezometrica; se agrega ahora el termino , que tiene también longitud y que viene dicho altura cinética. Ella de hecho representa por ejemplo, la altura del cual debe caer en el vacio originalmente en reposo para adquirir la velocidad v. La suma de la cota piezométrica y de la altura cinética viene indicada como trinomio de Bernoulli , condición tratada en la hidráulica tradicionalmente, carga total; se designa usualmente con la letra H
H= z + (p/pesp) + V2/2g ( V2 significa velocidad elevado al cuadrado )
Esta relación expresa el teorema de Bernoulli, que, teniendo presente todas las hipótesis que nos ha conducido a la formulación, podemos enunciar así; en el movimiento permanente de un fluido perfecto pesado incompresible la carga total se mantiene constante largo a cada trayectoria.
Interpretación geométrica y energía
El teorema de Bernoulli es susceptible de una inmediata interpretación geométrica. Consideramos la Fig. 5.5 una serie de puntos A,B, C,… sucesivamente junto a un elemento fluido que se mueve largo la propia trayectoria. Asumamos un plano horizontal de referimiento arbitrario, al cual atribuimos convencionalmente la cota z=0; a partir de eso, positivamente hacia lo alto, medimos las cotas geodésica za, zb, zc,…. De los puntos considerados. De los puntos mismos reportamos verticalmente hacia lo alto los segmentos de longitud igual a las alturas piezométricas pa/pesp, pb/pesp y pc/pesp.
Los extremos superiores A’, B’, C’,… estos segmentos y de los análogos correspondientes a todos los otros puntos de la trayectoria que no hemos explícitamente considerado, por obvia razones de la continuidad de las grandezas físicas en juego ( en particular de la presión ), si encontramos dispositivos largo a una línea continua, que llamamos línea piezométrica la trayectoria. La distancia de los sobre los puntos del plano de referimento equivale a la cota piezométrica de los correspondientes puntos de la trayectoria. Reportamos a partir de los puntos A’, B’, C’, … verticalmente hacia lo alto, segmentos de largueza igual a V2a/2g , V2b/2g y Vc2/2g , los extremos superiores de estos segmentos, se encuentran dispuestos largo la una línea, que diremos línea de las cargas totales de la trayectoria. El teorema de Bernoulli nos asegura que, en la hipótesis, esta línea pertenece a un plano horizontal; se tiene en efecto la norma de la formula siguiente: Fig 5-5
za + pa/pesp + V2a/2g= zb + pb/pesp + V2b/2g= zc + pc/pesp + V2c/2g= constante ( V2a significa elevado al cuadrado )
Fig. 5.5
El trazar las dos líneas que ahora hemos definido, piezométrica y las cargas totales, puede constituir un precioso auxilio para las resoluciones de muchos problemas practico y es útil a la correcta interpretación de los procesos hidráulicos .
Al teorema de Bernoulli puede también ser atribuido un preciso significado energético, que constituye la esencia y la importancia. Se puede en efecto demostrar que la carga total H representa la energía mecánica completa poseída de la unidad de peso del fluido en movimiento, le diremos energía especifica.
TSU Esp. Simón E. Ramos







0 comentarios:
Publicar un comentario
Por favor dejanos tus comentarios