RESISTORES INDUSTRIALES.También los resistores industriales se subdividen en fijos y variables y son dicho precisamente industriales; porque su precisión es tan lejana. Primero para hacer una lista de los resistores y reóstatos, veremos cuales son las grandezas que caracterizan a una resistores.
- tensión nominal ( Vn
- resistencia nominal ( Rn )
- potencia nominal ( Pn )
- tensión limite ( Vlim )
- resistencia critica ( Rc )
La tensión nominal Vn de una resistor nominal Rn, es aquella que corresponda a su potencia nominal Pn:
Pn Para un mismo modelo de resistor tiene una determinada Pn se tiene que aumentando Rn aumenta también Vn hasta un valor máximo, característico de aquel modelo de resistor, que viene definido por la tensión limite Vlim. La resistencia correspondiente es denominada resistencia critica Rc y vale:
Rc
La Vlim es por esto la tensión máxima que puede ser aplicada a la resistores la cual la resistencia sea igual o superior a aquella critica Rc.
Pertenecen a los resistores fijos industriales los:
1) Resistores a hilo, se obtiene bobinando en espiral sobre un soporte cerámico, un hilo de material resistivo, tienen normalmente valores de cualquier ohm, hasta 40 Kohm, con potencia nominal de 0,5 W hasta 8 W. La máxima corriente nominal es de un poco superior a 0,5 A.
2) Resistores químicos, obtenido de pasta de grafito, comprimido a grande presión y revestido de una sustancia aislante; alcanza a valores de decena de megaohm.
3) Regulación de la tensión en los circuitos de corriente continua.
Con mucha frecuencia las medidas en laboratorio, se debe regular la corriente en un circuito o la tensión que actúa en los terminales del circuito mismo; los dos problemas son en efecto coincidente por qué, esquematizando el circuito como un utilizador U cualquiera, de resistencia R, si se quiere regular la corriente circulante en U al valor I, ocurre regular la tensión en los terminales de U al valor RI.
a) Regulación con reóstato en serie.
El esquema usado es representado en la fig.. 75.
La batería de acumuladores suministra una tensión V1 ( que puede considerarse constante ) a los terminales del utilizador U de resistencia R en serie con el reóstato de regulación de resistencia completa o comprendida ( todas insertadas) R1. Se indica con r la parte de la resistencia insertada, la corriente I que circula por el utilizador, vale, por la ley de ohm:
3.2 I= V1/ ( r + R )
La corriente asume el valor máximo Imax cuando r=0 entonces nos queda 3.3 Imax= V1/ R.
La corriente asume el valor mínimo Imin cuando r=R1 , sustituyendo nos queda: 3’4 Imin= V1/ ( R1 + R )
1) Ejemplo.
Calcular la tensión al aplicar el valor de la resistencia del reóstato de campo de meter en serie con el circuito utilizador para regular la corriente de 0,5 a 2 A. La resistencia del circuito utilizador sea de 50 ohm.
se toma V1= RxImax= 50ohmx2A= 100 V, de la ecuación Imin= V1/ ( R1 + R ) entonces 0,5= 100 V / R1 + 50ohm
R1= 150 ohm.
El inconveniente de este sistema de regulación esta en la dificultad de realizar una bases de corrientes, por la cual ocurriera una resistencia elevada en el reóstato, especialmente si R es elevada. Se puede probar esta afirmación, dividiendo miembro a miembro las relaciones. 3.3 y 3.4 es decir:
3-5 Imax/Imin= (R1 + R )/ R Dividiendo numerador y denominador de la fracción al segundo miembro de la 3.5 por R, se obtiene 3.6 Imax/Imin= (R1/R) + 1 de la 3.6 prueba que se realiza amplia regulación
es decir grandes valores Imax/ Imin, ocurren grandes valores de R1/R; ejemplo para obtener Imin=(1/10)xImax, ocurre un reóstato de regulación de resistencia R1= 9R. La relación 3.2 representa la variación de I al variar r. Se indica con
la fracción de la resistencia insertada:
3.7 Si alfa=0 , cuando r=0 ( reóstato sin resistencia) y alfa= 1 cuando r=R1 ( reóstato completamente insertado). La relación 3.2 representa la variación de I al variar r, se indica con alfa la fracción de resistencia insertada.
alfa de la 3.2 se obtiene la siguiente formula .
Fig 75

1) Operando el cursor del reóstato R1 se lleva la corriente a un valor bastante cerca al deseado.
2) Operando sobre el cursor del reóstato R2 se regula definitivamente la corriente del valor deseado:
la operación resulta más fácil porque, a igualdad de longitud de los reóstatos, el mismodel
desplazamiento del cursor provoca sobre el reóstato R2 una variación de resistencia y por esto la
corriente es menor respecto al primero.
Para la escogencia de R1 y R2 hacemos el ejemplo siguiente:
Ejemplo. Se debe regular la tensión a los terminales de un circuito de la resistencia comprendida a 30 ohm
para valores comprendidos entre 15 y 90 V. Se calculan los valores de los dos reóstatos de regulación gruesa y fina, ahora se desea un cierto desplazamiento sobre el reóstato de regulación gruesa se obtiene la misma variación de tensión de un desplazamiento diez veces mayor sobre el reóstato de regulación fina.
Solución: Este ejemplo mete también en evidencia como los problemas de la tensión sean del todo análogo a los problemas de regulación de la corriente.
La tensión suministrada de la batería de acumuladores deberá ser al meno 90 V.
Suponemos ahora V1= 90 V, siendo Imax/Imin= 90/15= 6 , se obtiene. 6= (R1/R2) + 1 siendo R1=5R=5x30=150 ohm
Porque los dos reóstatos deben tener relación la igual a 10, si el primero tiene x , el otro tiene la resistencia 10x.
Pero: x + 10x= 150 ohm entonces, x= 150/11= 13,6 ohm
y 10x= 13,6x10= 136 ohm , como es obvio, los valores teóricos son 136 y 14 ohm, pero la selección efectiva dependerá de la disponibilidad del laboratorio, los valore encontrados son solo indicativo. también hemos podido hacer:
Imax= 90/30= 3 A , Imin= 15/30= 0,5 A
El esquema de la fig. 79, la tensión V1 de la batería de acumuladores es toda aplicada al reóstato de regulación R1. A los terminales del circuito utilizador ( U ) actúa una parte de la caída de tensión en lo largo de R1, si se indica con r la resistencia del reóstato de regulación comprendida entre los puntos N y B, se tiene que la resistencia comprendida del circuito entre los puntos N y M vale:
R1 - r + (Rxr)/( R + r ) y la corriente que comprende I1 es :
para la I aplicamos la ley de Kirchhoff en el nodo B: 3.10 I= I1-I2 de la otra parte.
Sustituyendo las relaciones 3.11 y 3.9 en la 3.10
Dela 3.11 se tiene:
Por la 3.10:
GALVANOMETROS:
El galvanómetros son instrumentos de laboratorio que sirven como reveladores de corriente muy débiles o medidas de corrientes y tensión del orden de los microamperios y de los micro voltios respectivamente. Su uso más importante es es como revelador de cero; sirve para establecer cuando en un ramo de un circuito no circula corriente. Es un instrumento indispensable para los métodos de medidas que se basan en los potenciómetros y los circuitos de puentes.
Los galvanómetros para corriente continua en uso actualmente son del tipo magnetoeléctrico ( dicho también galvanómetro Deprez d’Arsonval), es decir es a bobina móvil y magneto permanente.
PROTECCIONES A LOS GALVANÓMETROS:
Durante las medidas con galvanómetros, especialmente cuando vienen adaptado con indicadores de cero, ocurre proteger el equipo móvil con el fin de evitar ser dañada, una copia motriz muy elevada puede producir deformaciones mecánicas o rotura en la suspensión, similarmente un brusco golpe de corriente puede quemar la bobina.
Contra los peligros de una copia motriz muy intensa, se pone un shunt magnético aplicado a los lados de los polos magnéticos. Para proteger completamente la bobina se reduce la intensidad de corriente que atraviesa, aplicando una resistencia en paralelo ( shunt eléctrico ). La corriente I total, pasa en parte a través del galvanómetro y en parte a través del shunt. Se tiene en la fig. 116.
6.18 R.IR= r.Ig
Si indicamos con m, la relación de reducción, dicho también poder multiplicador así definido:
6.19 m= I/Ig
Se tiene:
6.20 m= (Ig + IR)/ Ig = 1 + IR/I
6.21 IR/Ig= r/R por la cual 6.22 m= 1 + r/R= ( R + r )/ R
La relación 6.22 permite obtener la relación de reducción obtenible con una resistencia R en paralelo, conocida la resistencia del galvanómetro y viceversa se puede encontrar a R conocido el poder multiplicador m, se tiene:
6.23 R= r/(m-1).
Ejemplo:
Un galvanómetro tiene resistencia interna de 500 ohm, cuanto valdrá la resistencia que se colocara en paralelo para reducir la corriente que a traviesa el galvanómetro a 1/20? Viceversa, cuanto vale la relación de reducción se se mete en paralelo una resistencia 9, 99 , 999 veces más pequeña?
Solución:
De la 6.23 se tiene el valor de la resistencia de poner en paralelo para obtener la relación de reducción igual a 20:
R= 500/(20-1)= 26,3 ohm
Para la segunda pregunta, indicando con m1, m2, m3 las relaciones de reducción obtenidas con resistencia en paralelo igual: (1/9)r, (1/99)r, (1/999)r respectivamente se tiene la relación 6.22.
Se tiene de la relación 6.22.
TERMOCOPIA.
Viene construido un circuito eléctrico cerrado, usando dos metales de diversa naturaleza, y llevan las dos juntas a diversas temperaturas, se nota que en este circuito se genera corriente eléctrica, o sea una f.e.m, con consecuencia circulación de corriente.
Si los dos metales son por ejemplo uno de cobre ( Cu ) y el otro de hierro ( Fe), ver la fig.1.
Si los dos metales son uno de cobre ( Cu ) y el otro de hierro ( Fe), ver la fig. 1, y las dos juntas son de temperatura diversas T1 y T2, donde T2 > T1, la circulación de la corriente será directa del cobre al hierro en la junta de más calor y del hierro al cobre en aquello de menos calor.
Se tiene por esto la formación de una f.e.m. al interno del circuito, cada vez que las juntas vienen llevadas a diversos grados de temperatura. Este fenómeno fue descubierto por el físico alemán THOMAS SEEBECK; toma el nombre de “ efecto Seebck’’.
La fuerza electromotriz generada depende de la naturaleza del material, por otra parte de manera esencial de la diferencia de temperatura existente entre las dos juntas.
La copia formada de los dos metales toma el nombre de “copia termoeléctrica” o “termocupla””, y las dos juntas vienen llamada “ juntas de calor” aquella a mayor temperatura y “juntas frías” aquellas a temperatura menor.
El fenómeno termoeléctrico, obedece a tres leyes fundamentales que son:
1) ley del circuito homogéneo
2) ley del circuito isotermo
1) Ley del circuito homogeneo.-
Un circuito formado de un único metal rigurosamente homogeneo, cualquiera sea la distribución de la temperatura aplicada a lo largo del metal, la f.e.m. es nula. Por lo tanto en una termocopia, constituida de dos metales perfectamente homogéneos, la f.e.m. generada no es dependiente de la distribución de la temperatura largo de ellos, pero solo de la
existente entre loa dos juntas.
2) Ley del circuito isotérmico.
En un circuito cerrado, formado de muchos metales , la sumatoria algebraica de todas las f.e.m. es nula , si el circuito es isotérmico.
Esta ley permite colocar un tercer metal en una termocopia, porque las dos nuevas juntas que se obtienen sean isotérmico, ver Fig. 2. En la termocopia constituida precedentemente de Cu-Fe, sustituimos un pedazo de Fe de Cu, la f.e.m. no varia se los dos nuevas juntas Cu-Fe son a la misma temperatura ( t3). Aprovechando este principio, se puede sustituir el pedacito de Cu en el circuito de un galvanómetro, y leer así el valor de la f.e.m. sin posibilidad de alterar el régimen de funcionamiento de dicha termocopia.
Generalmente los elementos más usados en la construcción de las termocopia son ligado al alto potencial termoeléctrico, fácilmente repetible, inoxidable y alto punto de fusión.
Las copias termoeléctrica más comúnmente usadas son las siguientes;
- Cobre- Constantan ………………………………….. de – 200 a 500 grados centígrados
- Hierro- Constantan -------------------------- de – 200 a 700 ‘’ “
- Niquelcromo-Constantan-------------------- hasta “ “
- Niquelcromo-Níquel -------------------------- hasta 1000 ” ”
- Chromel-Alumel ------------------------------- hasta 1200 ” ”
- Platinorodio-Platino ---------------------------- hasta 1600 ” ”
- Platinorodio-Platinorodio ----------------------- hasta 1800 ” ”
- volframio=Tungsteno-Tantalio ------------------ hasta 2000 ” ”
- Volframio-Molibdeno ------------------------------ hasta 2500 ” ”
- Tantalio-Volframio Molibdeno--------------------- hasta 2900 ” ”
El primer metal o liga asume siempre como polo positivo y el segundo polo negativo. ( Es.: no.1, Cobre- Constantan: el cobre constituye el polo positivo, mientras la constantan el polo negativo; la no.5, Chromel-Alumel: el Chromel constituye el polo positivo, mientras que el Alumel es el polo negativo, etc.
Entre las varias termocopia visto hasta ahora, la más precisa es aquella de platino Rodio-Platino, porque mantiene constante en el tiempo sus características no presentan fenómenos de envejecimiento particularmente apreciable.
Su costo elevado no limita el uso solo por la altísima temperatura,o también como termocopia modelo.
Como dicho precedentemente,el potencial termoeléctrico ( o la tensión eléctrica de la copia termoeléctrica) es el resultante de la diferencia de los valores indicados, por los varios metales, en mV, de la tabla que sigue, en la cual los potenciales termoeléctricos son estado establecidos tomando como metal de referencia el platino, atribuyéndole el potencial mas o menos 0 mV y fijando en 100 grados centígrados la diferencia de temperatura entre la junta fría y aquella caliente.
- platino ---------------------- más o menos 0 mV
- Cobre ------------------------da 0,72 a 0,77 ”
- Costantan----------- menos 3,47 a menos 3,04 ”
- Hierro -------------------- de 1,87 a 1,89 a 1,89 ”
- Niquelcromo --------------------- 2,2 ”
- Niquel --------------de menos 1,94 a menos 1,2 ”
- Cromo ------------- de 0,040 a 0,043 ”
- Rodio --------------------- 0,65 ”
- Wolframio ---------de 0,65 a 0,9 ”
- Tantalio ---------- de 0,34 a 0,51 ”
- Molibdeno ------ de 1,16 a 1,31 ”
- Alumel -------- de 0,038 a 0,041 ”
- Plata ---------- de 0,67 a 0,79 ”
- Zinc --------- de 0,69 a 0,79 ”
- Iridio ------- de 0,65 a 0,68 ”
- Mercurio ---de menos 0,07 a 0,04 ”
METODOS DE MEDIDA DE LA POTENCIA ACTIVA, REACTIVA Y FACTOR DE POTENCIA.
Simultáneamente veremos que en los sistemas trifásicos existen métodos de medidas de la potencia más usadas en laboratorio, de los métodos directos con instrumentos trifásicos. De la otra parte los vatímetros y los varímetros trifásicos reasumiendo en su interno la conexión entre varios instrumentos monofásicos.
De aquí la necesidad de examinar a fondo los diversos métodos de medidas de la potencia y del factor de potencia.
Las medidas de energía, que veremos posterior, se basan sobre los mismos métodos que estamos por examinar. Esta es otra de las razones que veremos mas adelante la importancia fundamental en el campo de la medidas eléctrica.
METODO DE POTENCIA EN CORRIENTE CONTINUA.
El método directo de medida de la potencia en corriente continua requiere el uso de un vatímetro ( obviamente el vatímetro debe ser de tipo adecuado a funcionar en c.c. ejemplo un vatímetro electrodinámico, no un vatímetro a inducción) conectado como aparece en la fig. 3, como ya se ha dicho, para evitar que el instrumento sea sobrecargado, se conecta un voltímetro y un amperímetro para controlar que la corriente y la tensión no superen la capacidad del vatímetro.Pero el voltímetro y el amperímetro, que ocurre a insertar en cada caso, son ya suficiente para medir la potencia, por esto usamos un voltímetro y un amperímetro magnetoeléctrico disponible también en clase mucha calidad y bajo autoconsumo, se puede quitar el vatímetro y aplicar los esquemas de la Fig.4 a y b: este método se llama vol-amperímetro.
Indicando con V e I la tensión y la corriente medidas en los instrumentos, se puede calcular la potencia generada y la potencia utilizada mediante la fórmula:
6.1) Pm=Pg=Pu= V I
La 6.1 es aproximada en cuanto no tiene en cuenta de los errores sistemáticos debido al consumo de los instrumentos. Estos errores sistemáticos pueden ser evaluados y eventualmente eliminados en modo análogo aquellos seguidos por el vatímetro.
Identificación:
Ig= corriente generada del generador
Vg= tensión en los terminales del generador
Iu= corriente absorbida del utilizador
Vu= tensión en los terminales del utilizador
Iv= corriente absorbida del voltímetro
Rv= resistencia interna del voltímetro
Va= caída de tensión en el amperímetro
Ra= resistencia interna del amperímetro
Pg= potencia generada
Pu= potencia utilizada
Pm= potencia medidas
Pa= potencia consumida el amperímetro
Pv= potencia consumida el voltímetro
se puede escribir:
6.2)
Mediante la 6.2) se puede calcular la potencia consumida de los instrumentos en base a la lectura y que sea conocida su resistencias internas.Las potencias se calculan de la manera siguiente:
a) voltímetro ante el amperímetro ver Fig.4-a.
b) voltímetro después del amperímetro. Ver Fig. 4.b,
Para recordar las formulas procedentes basta tener presente que, para calcular la potencia generada ocurre agregar al valor medido la potencia consumida del instrumento puesto ante del amperímetro ( voltímetro); mientras para calcular la potencia utilizada ocurre quitar el valor medido de la potencia consumida del instrumento puesto después del amperímetro ( voltímetro). La resistencia interna Ra del amperímetro varia con la temperatura siendo de cobre, por esto la valuación de Pa mediante la 6.2, es mas que todo insertada; al contrario el valor de la resistencia Rv del voltímetro se puede considerar independiente de la temperatura siendo en prevalencia la manganina, por esto la valuación de Pv en la 6.2, resulta bastante exacta. Por esta razón, ahora si se efectúa la corrección de la medida como dicho precedentemente, es mejor usar las formulas 6.3 y 6.6, de la fig. 4-b, para la potencia utilizada.
Si no se desea aportar corrección al valor medido conviene la inserción que da lugar a menor error: generalmente se puede decir, teniendo presente la 6.2) que por baja corriente y alta tensiones Pa es bajo y Pv es alto por esto conviene el esquema Fig. 4 b para la medida de Pu; viceversa para la alta corriente y baja tensión.
En la práctica se escoge la conexión que se supone mejor en base a cuanto se a dicho para evaluar el error porcentual con la siguiente formula:
6.7) Er%= [(Pm – P) / P]x100=[ (Pm-P)/Pm ]x100 donde Pm es el valor medido y P el valor correcto.
Si el error es debido al autoconsumo del amperímetro, se tiene el signo que puede ser positivo o negativo.
6.8) Er%= (Pa/P)x100= (Pa/Pm)x100= [(VaxI)/(VxI)]x100= (Va/V)x100
y si el error es debido al autoconsumo del voltímetro, se puede tener el signo menos o mas.
6.9) Er%= (Pv/P)x100= (Pv/Pm)x100= [(VxIv)/(VxI)]x100= (Iv/I)x100
El error porcentual supera el máximo tolerable, se cambia la inserción o se aporta la necesaria corrección.
Las formulas 6.8 y 6.9) pueden servir también para reconocer aproximadamente la mejor inserción.
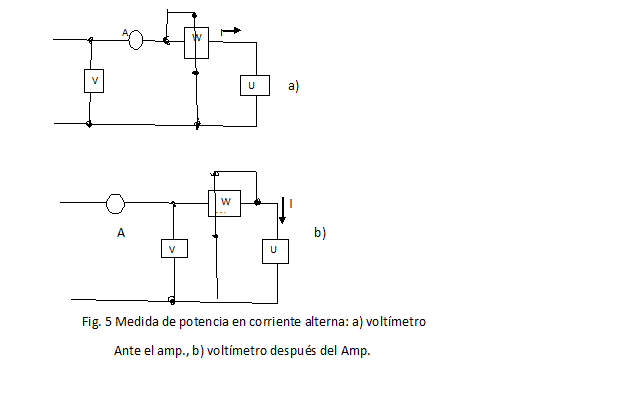
MEDIDA DE POTENCIA Y DEL FACTOR DE POTENCIA EN CORRIENTE ALTERNA MONOFASICA.
La medida de potencia activa en un circuito a corriente alterna monofásica se efectúa por vía directa mediante el uso de un vatímetro.
El esquema de conexión es el de la Fig. 5 , son posible las dos inserciones ver Fig.5 a y b correspondiente a voltímetro ante el amperímetro y el voltímetro después del amperímetro.
En el esquema son previsto un amperímetro y un voltímetro, también de clase no de calidad, para controlar que el vatímetro no sea sobrecargado . Estos dos instrumentos son estado ante del vatímetro para no influenciar la lectura supuesto de querer medir la potencia consumida en el usuario; obviamente en el caso se quiera medir una potencia generada ocurre inserirle el voltímetro y el amperímetro ante el vatímetro, la lectura del vatímetro es afectada de un error sistemático, de hecho con la inserción Fig.5 a el instrumento marca en más la potencia consumida de la bobina amperimétrica.:
Mientras con la inserción Fig. 5 b, el instrumento marca más la potencia consumida en su bobina voltimétrica ecua. 6.11
mientras con la inserción de la Fig. 5 b, el instrumento indica más la potencia consumida de la bobina voltimétrica.
Mediante las formulas 6.10 y 6.11, se puede aportar las relativas correcciones al valor de la potencia medida.El fin correctivo del calculo que influye sobre una parte mínima del valor medido, se puede asumir como valores de I y V en las formulas procedentes los valores indicado del amperímetro y del voltímetro. Para la selección de la mejor inserción, vale la consideración dicha mas veces.
Para la potencia reactiva, la potencia aparente y el factor de potencia de la carga es mejor usar el esquemas de la Fig.6 a y b correspondientes a voltímetro primero y voltímetro después.
Si los consumos de los instrumentos pueden considerar insignificante, dichos V, I y P respectivamente. Formula 6.12)
Siendo A , Q y cosfi respectivamente potencia aparente, potencia reactiva y factor de potencia de la carga.
Si los consumos de los instrumentos no son insignificante; ocurre transferir la corrección con las formulas usando el esquema de la Fig. 6 b, siendo la más exacta para la determinación de los autoconsumos.
Ejemplo. los valores medidos de los tres instrumentos como en Fig.6 b son:
V= 100 V; I= 2 A ; P= 150 W
Las resistencias del voltímetro y del vatímetro son: Rv1= 5000 ohm y Rv2= 15000 ohm. Se quiere calcular la potencia consumida sobre el usuario y el factor de potencia.
solución: Las potencias consumida sobre el circuito voltímetro y del vatímetro , valen respectivamente:
La potencia exacta vale:
P= ( 150- 2- 0,67 )= 147,33 W.
El cálculo exacto de I es complejo en cuanto ocurre quitar vectorialmente a la corriente indicada en el amperímetro las corriente absorbida de los circuitos voltimétricos . renunciando al aporte de la corrección se tiene:
A= V I = 100 V x 2 A = 200 VA
Elaborado: por el T.S.U.Esp. Simón E. Ramos
Comentario al: hazelectronica@gmail.com
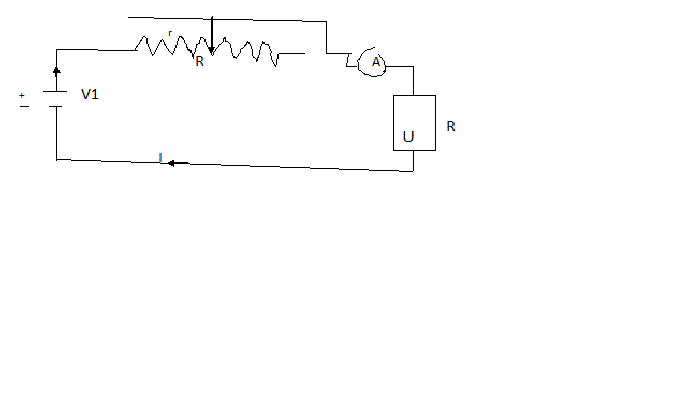
![clip_image002[5] clip_image002[5]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiLrnn85aUkgcYoXiG9lJOVr7gZ8eUbyfOlh043jJFUxOHkE5S9Zr9xkZez0DKUeLdAy8zyXtut6ZGiA_YOZzEIqLqTTrY5h9HQZC5lNaN-VaotnejL0DZ0FVQVfcNmO2wkk_ZJRfxZpilN/?imgmax=800)
![clip_image002[1] clip_image002[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgTVKchiB_-RhTWJj_cC2AcnOEcAKNm51w985OZfYkwBvDWgS1r4rku2W02HJyR3tH-Y7PofhvinC1xZ6XkUluhw40mF8BFjpOs6uaFXXgSFwv67bJvfUKcwA2CtcknQYfaUPa2rsS4Y4bP/?imgmax=800)

![clip_image002[1] clip_image002[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEggFJlZvnJ1C4AHtIN7cUNzT3jXqxXhQocSs7vTz4c108saThPI3h_BHU9hh6k52GbRjcEped9Vv2amhTlLlnoytCy_ypZxsF-lPWt6raI1I8fqSlkswgPDoCzxQS2FA6mA6xAuGSOiEtaU/?imgmax=800)

![clip_image002[1] clip_image002[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjLC-jnuGQyWhqVGkapmTja863043umJDqAR1YZBsKmKkPTVXDaFMmv6TLlTg8iGSy0L6dOr-t2P3OIlM_QWsWTd_yaIEeGLPQlxU66HRseVwfhS_LpD7FQ6NY_qEhHOOdjXkS2IHdfJQgg/?imgmax=800)
![clip_image008[1] clip_image008[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEioXZz4b-T6M8z3f8NbzEXMMQFh31zhLmjFZOFlwjepaOJqknx1lJU060KwUF3Y7kepMMCreTOEhVyQ4saAwD15JIVCh3j4PHayEq8HQ__SCog1TDj9o7BlWvGq3jFNDLgxkvJGlnjYnJPv/?imgmax=800)
![clip_image010[1] clip_image010[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj_iyvMRu7DvHH2aHJINymY7T67TH-jUytBO4YRkpcFtL1eIHqczaPgxCtA_ciNPx7I0i4fOUC0QXH4tIGWjy5rFXHZuDzdX9QiF3Das8_8FzlPWbIeLB8qSMB7T_-haq5_xO6Oku5NgX0G/?imgmax=800)